Sacred Geometry
How to Create a Multiverse

It unites the mind and the heart (called the "intelligence of the heart" by the ancient Egyptians), spirit and matter, science and spirituality. These are all apparently separate halves of the Whole. Plato said in the Republic (VII, 527 d, e) that it is through geometry that one purifies the eye of the soul, "since it is by it alone that we contemplate the truth." Mother nature uses geometry everywhere you look, from the spirals of the nautilus shell, sunflower centre and spiral galaxies to the hexagon symmetry of snowflakes, flower petals and honeycomb. Geometry in nature arranges the shapes of the molecules and crystals that make up our bodies and the physical cosmos. It is the key to the creation of the universe. A good primer on this subject is Michael Schneiders interesting book A Beginner's Guide to Constructing the Universe. In his introduction, he says: "It's a shame that children are exposed to numbers merely as quantities instead of qualities and characters with distinct personalities relating to each other in various patterns. If only they could see numbers and shapes as the ancients did, as symbols of principles available to teach us about the natural structure and process of the universe and to give us perspective on human nature."
|
|
From Wholesome Balance @ http://geometry.wholesomebalance.com/index.html & http://geometry.wholesomebalance.com/Sacred_Geometry_2.html
Sacred Geometry Introductory Tutorial
by Bruce Rawles
In nature, we find patterns, designs and structures from the most minuscule particles, to expressions of life discernible by human eyes, to the greater cosmos. These inevitably follow geometrical archetypes, which reveal to us the nature of each form and its vibrational resonances. They are also symbolic of the underlying metaphysical principle of the inseparable relationship of the part to the whole.
It is this principle of oneness underlying all geometry that permeates the architecture of all form in its myriad diversity. This principle of interconnectedness, inseparability and union provides us with a continuous reminder of our relationship to the whole, a blueprint for the mind to the sacred foundation of all things created.
The Sphere
Starting with what may be the simplest and most perfect of forms, the sphere is an ultimate expression of unity, completeness, and integrity. There is no point of view given greater or lesser importance, and all points on the surface are equally accessible and regarded by the center from which all originate. Atoms, cells, seeds, planets, and globular star systems all echo the spherical paradigm of total inclusion, acceptance, simultaneous potential and fruition, the macrocosm and microcosm.
The Circle
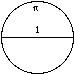
The circle is a two-dimensional shadow of the sphere which is regarded throughout cultural history as an icon of the ineffable oneness; the indivisible fulfillment of the Universe. All other symbols and geometries reflect various aspects of the profound and consummate perfection of the circle, sphere and other higher dimensional forms of these we might imagine.
The ratio of the circumference of a circle to its diameter, Pi, is the original transcendental and irrational number. (Pi equals about 3.14159265358979323846264338327950288419716939937511…) It cannot be expressed in terms of the ratio of two whole numbers, or in the language of sacred symbolism, the essence of the circle exists in a dimension that transcends the linear rationality that it contains. Our holistic perspectives, feelings and intuitions encompass the finite elements of the ideas that are within them, yet have a greater wisdom than can be expressed by those ideas alone.
The Point
.
At the center of a circle or a sphere is always an infinitesimal point. The point needs no dimension, yet embraces all dimension. Transcendence of the illusions of time and space result in the point of here and now, our most primal light of consciousness. The proverbial “light at the end of the tunnel” is being validated by the ever-increasing literature on so-called “near-death experiences”. If our essence is truly spiritual omnipresence, then perhaps the “point” of our being “here” is to recognize the oneness we share, validating all “individuals” as equally precious and sacred aspects of that one.Life itself as we know it is inextricably interwoven with geometric forms, from the angles of atomic bonds in the molecules of the amino acids, to the helical spirals of DNA, to the spherical prototype of the cell, to the first few cells of an organism which assume vesical, tetrahedral, and star (double) tetrahedral forms prior to the diversification of tissues for different physiological functions. Our human bodies on this planet all developed with a common geometric progression from one to two to four to eight primal cells and beyond.
Almost everywhere we look, the mineral intelligence embodied within crystalline structures follows a geometry unfaltering in its exactitude. The lattice patterns of crystals all express the principles of mathematical perfection and repetition of a fundamental essence, each with a characteristic spectrum of resonances defined by the angles, lengths and relational orientations of its atomic components.
The Square Root of Two
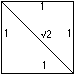
The square root of 2 embodies a profound principle of the whole being more than the sum of its parts. (The square root of two equals about 1.414213562…) The orthogonal dimensions (axes at right angles) form the conjugal union of the horizontal and vertical which give birth to the greater offspring of the hypotenuse. The new generation possesses the capacity for synthesis, growth, integration and reconciliation of polarities by spanning both perspectives equally. The root of two originating from the square leads to a greater unity, a higher expression of its essential truth, faithful to its lineage.
The fact that the root is irrational expresses the concept that our higher dimensional faculties can’t always necessarily be expressed in lower order dimensional terms – e.g. “And the light shineth in darkness; and the darkness comprehended it not.” (from the Gospel of St. John, Chapter 1, verse 5). By the same token, we have the capacity to surpass the genetically programmed limitations of our ancestors, if we can shift into a new frame of reference (i.e. neutral with respect to prior axes, yet formed from that matrix-seed conjugation. Our dictionary refers to the word matrix both as a womb and an array (or grid lattice). Our language has some wonderful built-in metaphors if we look for them!
The Golden Ratio
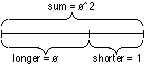
The golden ratio (a.k.a. phi ratio a.k.a. sacred cut a.k.a. golden mean a.k.a. divine proportion) is another fundamental measure that seems to crop up almost everywhere, including crops. (The golden ratio is about 1.618033988749894848204586834365638117720309180…) The golden ratio is the unique ratio such that the ratio of the whole to the larger portion is the same as the ratio of the larger portion to the smaller portion. As such, it symbolically links each new generation to its ancestors, preserving the continuity of relationship as the means for retracing its lineage.
The golden ratio (phi) has some unique properties and makes some interesting appearances:
- phi = phi^2 – 1; therefore 1 + phi = phi^2; phi + phi^2 = phi^3; phi^2 + phi^3= phi^4; ad infinitum.
- phi = (1 + square root(5)) / 2 from quadratic formula, 1 + phi = phi^2.
- phi = 1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/…)))))
- phi = 1 + square root(1 + square root(1 + square root(1 + square root(1 + square root(1 + …)))))
- phi = (sec 72)/2 =(csc 18)/2 = 1/(2 cos 72) = 1/(2 sin 18) = 2 sin 54 = 2 cos 36 = 2/(csc 54) = 2/ (sec 36) for all you trigonometry enthusiasts.
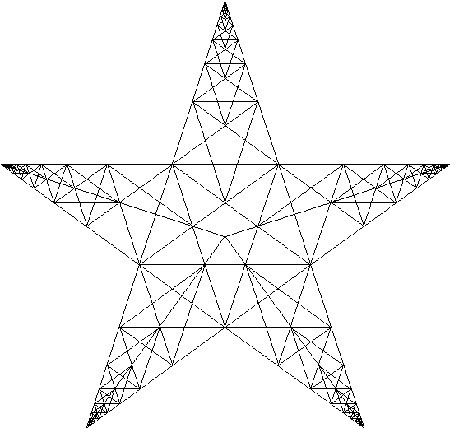
- phi = the ratio of segments in a 5-pointed star (pentagram) considered sacred to Plato and Pythagoras in their mystery schools. Note that each larger (or smaller) section is related by the phi ratio, so that a power series of the golden ratio raised to successively higher (or lower) powers is automatically generated: phi, phi^2, phi^3, phi^4, phi^5, etc.
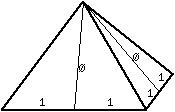
- phi = apothem to bisected base ratio in the Great Pyramid of Giza
- phi = ratio of adjacent terms of the famous Fibonacci Series evaluated at infinity; the Fibonacci Series is a rather ubiquitous set of numbers that begins with one and one and each term thereafter is the sum of the prior two terms, thus: 1,1,2,3,5,8,13,21,34,55,89,144… (interesting that the 12th term is 12 “raised to a higher power”, which appears prominently in a vast collection of metaphysical literature)
The mathematician credited with the discovery of this series is Leonardo Pisano Fibonacci and there is a publication devoted to disseminating information about its unique mathematical properties, The Fibonacci Quarterly
Fibonacci ratios appear in the ratio of the number of spiral arms in daisies, in the chronology of rabbit populations, in the sequence of leaf patterns as they twist around a branch, and a myriad of places in nature where self-generating patterns are in effect. The sequence is the rational progression towards the irrational number embodied in the quintessential golden ratio.
This most aesthetically pleasing proportion, phi, has been utilized by numerous artists since (and probably before!) the construction of the Great Pyramid. As scholars and artists of eras gone by discovered (such as Leonardo da Vinci, Plato, and Pythagoras), the intentional use of these natural proportions in art of various forms expands our sense of beauty, balance and harmony to optimal effect. Leonardo da Vinci used the Golden Ratio in his painting of The Last Supper in both the overall composition (three vertical Golden Rectangles, and a decagon (which contains the golden ratio) for alignment of the central figure of Jesus.
The outline of the Parthenon at the Acropolis near Athens, Greece is enclosed by a Golden Rectangle by design.
The Square Root of 3 and the Vesica Piscis
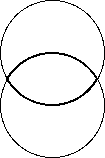
The Vesica Piscis is formed by the intersection of two circles or spheres whose centers exactly touch. This symbolic intersection represents the “common ground”, “shared vision” or “mutual understanding” between equal individuals. The shape of the human eye itself is a Vesica Piscis. The spiritual significance of “seeing eye to eye” to the “mirror of the soul” was highly regarded by numerous Renaissance artists who used this form extensively in art and architecture. The ratio of the axes of the form is the square root of 3, which alludes to the deepest nature of the triune which cannot be adequately expressed by rational language alone.
Spirals
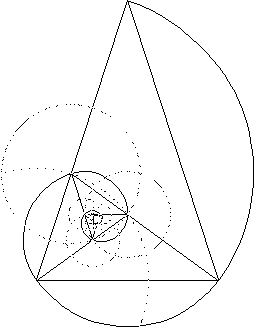
This spiral generated by a recursive nest of Golden Triangles (triangles with relative side lengths of 1, phi and phi) is the classic shape of the Chambered Nautilus shell. The creature building this shell uses the same proportions for each expanded chamber that is added; growth follows a law which is everywhere the same. The outer triangle is the same as one of the five “arms” of the pentagonal graphic above.
Toroids

Rotating a circle about a line tangent to it creates a torus, which is similar to a donut shape where the center exactly touches all the “rotated circles.” The surface of the torus can be covered with 7 distinct areas, all of which touch each other; an example of the classic “map problem” where one tries to find a map where the least number of unique colors are needed. In this 3-dimensional case, 7 colors are needed, meaning that the torus has a high degree of “communication” across its surface. The image shown is a “birds-eye” view.
Dimensionality
The progression from point (0-dimensional) to line (1-dimensional) to plane (2-dimensional) to space (3-dimensional) and beyond leads us to the question – if mapping from higher order dimensions to lower ones loses vital information (as we can readily observe with optical illusions resulting from third to second dimensional mapping), does our “fixation” with a 3-dimensional space introduce crucial distortions in our view of reality that a higher-dimensional perspective would not lead us to?
Fractals and Recursive Geometries
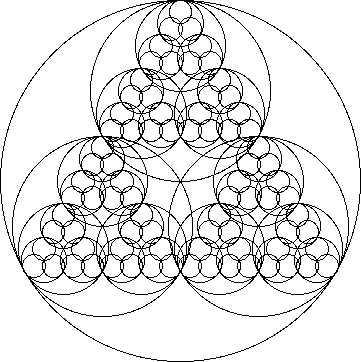
There is a wealth of good literature on this subject; it’s always fascinating how nature propagates the same essence regardless of the magnitude of its expression…our spirit is spaceless yet can manifest aspects of its individuality at any scale.
Perfect Right Triangles
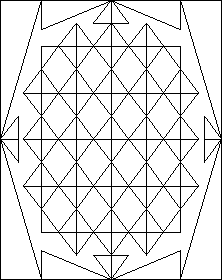
The 3/4/5, 5/12/13 and 7/24/25 triangles are examples of right triangles whose sides are whole numbers. The graphic above contains several of each of these triangles. The 3/4/5 triangle is contained within the so-called “King’s Chamber” of the Great Pyramid, along with the 2/3/root5 and 5/root5/2root5 triangles, utilizing the various diagonals and sides.
The Platonic Solids
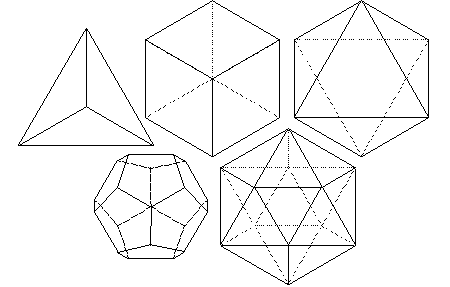
The 5 Platonic solids (Tetrahedron, Cube or (Hexahedron), Octahedron, Dodecahedron and Icosahedron) are ideal, primal models of crystal patterns that occur throughout the world of minerals in countless variations. These are the only five regular polyhedra, that is, the only five solids made from the same equilateral, equiangular polygons. To the Greeks, these solids symbolized fire, earth, air, spirit (or ether) and water respectively. The cube and octahedron are duals, meaning that one can be created by connecting the midpoints of the faces of the other. The icosahedron and dodecahedron are also duals of each other, and three mutually perpendicular, mutually bisecting golden rectangles can be drawn connecting their vertices and midpoints, respectively. The tetrahedron is a dual to itself.
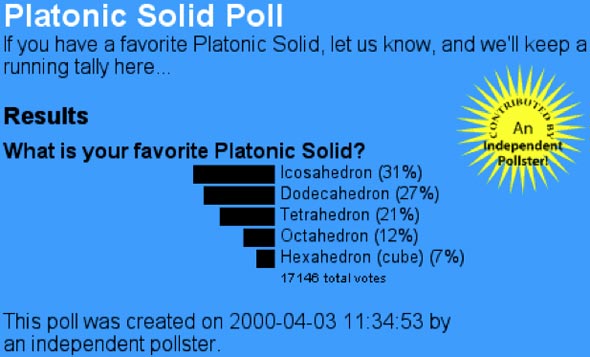
From April, 2000 through (at least) December, 2003, we conducted a poll on which Platonic Solid folks liked best; here’s the results from that period. If there’s interest, I’ll start another poll to see if the preferences has shifted!
Here are some animations of counter-rotating polyhedra and images of the Platonic solids showing their relationships as duals.
Here are fold-up patterns for the Platonic Solids.
The Archimedean Solids
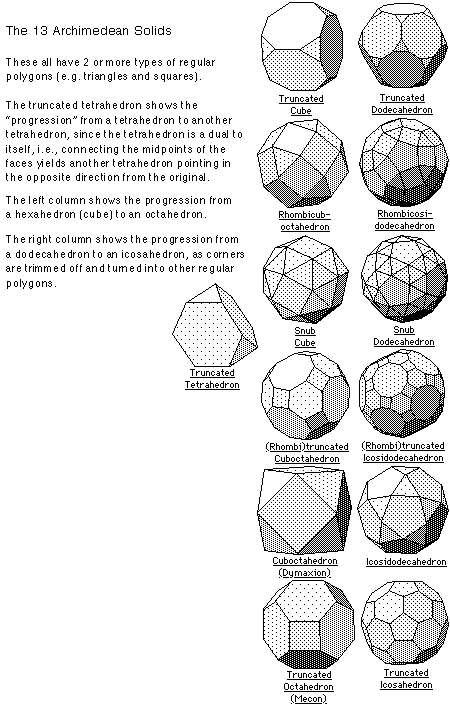
There are 13 Archimedean solids, each of which are composed of two or more different regular polygons. Interestingly, 5 (Platonic) and 13 (Archimedean) are both Fibonacci numbers, and 5, 12 and 13 form a perfect right triangle.
Stellations of The Platonic Solids and The Archimedean Solids

This is a stellation of a dodecahedron where each pentagonal face is capped with a pentagonal pyramid composed of 5 golden triangles, a sort of 3-dimensional 5-pointed star.
Here are more images of polyhedra (Platonic and Archimedean Solids.)
Metatron’s Cube
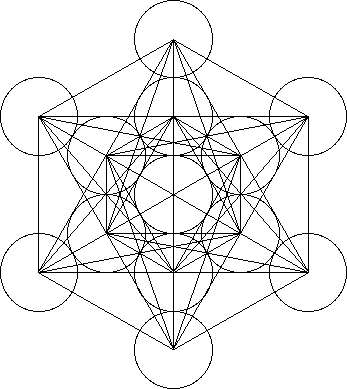
Metatron’s Cube contains 2-dimensional images of the Platonic Solids (as shown above) and many other primal forms.
The Flower of Life
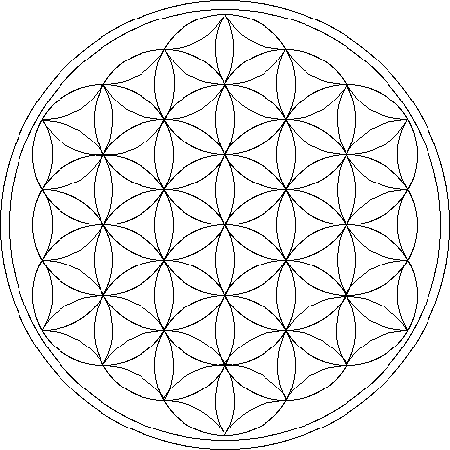
Indelibly etched on the walls of temple of the Osirion at Abydos, Egypt, the Flower of Life contains a vast Akashic system of information, including templates for the five Platonic Solids. The background graphic for this page is a repetitive hexagonal grid based on the Flower of Life.

From The Geometry Code @ http://www.geometrycode.com/sacred-geometry/
The Fibonacci Sequence
edieval mathematician and businessman Fibonacci (Leonardo Pisano) posed the following problem in his treatise Liber Abaci (pub. 1202):
How many pairs of rabbits will be produced in a year, beginning with a single pair, if in every month each pair bears a new pair which becomes productive from the second month on?
It is easy to see that 1 pair will be produced the first month, and 1 pair also in the second month (since the new pair produced in the first month is not yet mature), and in the third month 2 pairs will be produced, one by the original pair and one by the pair which was produced in the first month. In the fourth month 3 pairs will be produced, and in the fifth month 5 pairs. After this things expand rapidly, and we get the following sequence of numbers:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
This is an example of a recursive sequence, obeying the simple rule that to calculate the next term one simply sums the preceding two:
F(1) = 1
F(2) = 1
F(n) = F(n – 1) + F(n – 2)
Thus 1 and 1 are 2, 1 and 2 are 3, 2 and 3 are 5, and so on.

Here we have taken squares with sides whose lengths correspond to the terms of the Fibonacci sequence, and arranged them in an “outwardly spiraling” pattern. Notice that the rectangles which result at each stage are all roughly the same shape, that is, that the ratio of length to width seems to “settle down” as we build the pattern outward. Notice also that the ratio of length to width is at every step the ratio of two successive terms of the Fibonacci sequence, that is, the ratio of the greater one to the lesser. These ratios may be thought of as forming a new sequence, the sequence of ratios of consecutive Fibonacci numbers:
This sequence converges, that is, there is a single real number which the terms of this sequence approach more and more closely, eventually arbitrarily closely. We may discover this number by exploiting the recursive definition of the Fibonacci sequence in the following way. Let us denote the nth term of the sequence of ratios by xn, that is,
Then using the recursive definition of F(n) given above, we have:

Now supposing for the moment that the sequence converges to a real number x (a fact which requires proof, but we'll leave that aside), we may observe that both xn and
Consequently, the real number x to which the sequence of ratios converges must satisfy the following equation:
This is a simple equation to solve for x: it is really a quadratic equation, and its positive root is the value we are looking for:


The growth of this nautilus shell, like the growth of populations and many other kinds of natural “growing,” are somehow governed by mathematical properties exhibited in the Fibonacci sequence. And not just the rate of growth, but the pattern of growth. Examine the crisscrossing spiral seed pattern in the head of a sunflower, for instance, and you will discover that the number of spirals in each direction are invariably two consecutive Fibonacci numbers.

From Math Academy @ http://www.mathacademy.com/pr/prime/articles/fibonac/index.asp
Please Help Keep This Unique Site Online
Donate any amount and receive at least one New Illuminati eBook!
For further enlightening information enter a word or phrase into the search box @ New Illuminati or click on any label/tag at the bottom of the page @ http://nexusilluminati.blogspot.com
And see
New Illuminati – http://nexusilluminati.blogspot.com
New Illuminati on Facebook - http://www.facebook.com/pages/New-Illuminati/320674219559
New Illuminati Youtube Channel - http://www.youtube.com/user/newilluminati/feed
The Her(m)etic Hermit - http://hermetic.blog.com
This material is published under Creative Commons Fair Use Copyright (unless an individual item is declared otherwise by copyright holder) – reproduction for non-profit use is permitted & encouraged, if you give attribution to the work & author - and please include a (preferably active) link to the original along with this notice. Feel free to make non-commercial hard (printed) or software copies or mirror sites - you never know how long something will stay glued to the web – but remember attribution! If you like what you see, please send a tiny donation or leave a comment – and thanks for reading this far…
From the New Illuminati – http://nexusilluminati.blogspot.com

















This will be the 3rd time I try to publish my thoughts, interesting 3 times 3 sides.. I have a long interesting story how I found your blog and why I stayed. The answer to Lady Leto's Flame, is your Qi energy. Meditate, focus on a specific crystal structure, and imbue it with your Flame. Some monk's chant into Chi or Qi state to presumably float or focus self-structural points of energy, so if you can generate Qi, you focus not out but in. Well seemed like the answer, and I found answers here, so thank you
ReplyDeletehttp://www.academia.edu/8991727/Phenomenal_World_as_an_Output_of_Cognitive_Quantum_Grid_Theory_of_Everything_using_Leibniz_Kant_and_German_Idealism
ReplyDeleteDr OBUDU have been a great doctor even know in the world, am here today to tell the world my testimony about how i was cured from herpes.i was having this deadly disease called herpes in my body for the past 6 years but now i know longer have it again. i never know that this disease have cure not until i meet someone know to the world called Dr OBUDU he cured me from herpes he have been great to me and will also be great to you too. i have work with other doctor but nothing come out. one day i did a research and came across the testimony of a lady that also have same disease and got cured by Dr OBUDU. then i contacted his email and told him my problem.he told me not to worry that he have the cure i didn't believe him when he said so because my doctor told me there is no cure.he told me i need to get a herbal medicine for the cure which i did and now am totally cured you can also be cured of any other diseases too if only you believe in him. contact him via email OBUDU.MIRACLEHERBALHOME@GMAIL.COM you can also call or whatsapp him true his mobile number +2347035974895
ReplyDelete